quarta-feira, 30 de novembro de 2011
Atividades sobre propriedades dos determinantes
1.O valor do determinante  é:
é:
a)
b)
c)
d)
e)
2. Seja A ∈ Mn (R) e |A| = 2. Determine:
a) A2
b) |3A|
c) A−1
d) Ak
e) A
 é:
é:a)
b)
c)
d)
e)
2. Seja A ∈ Mn (R) e |A| = 2. Determine:
a) A2
b) |3A|
c) A−1
d) Ak
e) A
Propriedades dos Determinantes
As propriedades envolvendo determinantes facilitam o cálculo de seu valor em matrizes que se enquadram nessas condições. Observe as propriedades:
Caso ocorra igualdade de elementos entre duas linhas ou duas colunas, o determinante dessa matriz será nulo.
Ao multiplicarmos todos os elementos de uma linha ou coluna de uma matriz por um número K, o seu determinante fica multiplicado por K.
Caso uma matriz quadrada A seja multiplicada por um número real k, seu determinante passa a ser multiplicado por kn.
O valor do determinante de uma matriz R é igual ao determinante da matriz da transposta de R, det R = det (Rt).
7ª propriedade
O determinante de uma matriz triangular é igual à multiplicação dos elementos da diagonal principal. Lembre-se que em uma matriz triangular, os elementos acima ou abaixo da diagonal principal são iguais a zero.
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.
Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jaco.
1ª propriedade
Ao observar uma matriz e verificar que os elementos de uma linha ou uma coluna são iguais a zero, o valor do seu determinante também será zero.2ª propriedade
3ª propriedade
Verificadas em uma matriz duas linhas ou duas colunas com elementos de valores proporcionais, o determinante terá valor igual à zero. Observe a propriedade entre a 1ª e a 2ª linha.
4ª propriedade
Os elementos da 1ª linha de P foram multiplicados por 2, então: det P’ = 2 * det P
5ª propriedade
6ª propriedade
det R = ps -- qr
det Rt = ps – rq
det Rt = ps – rq
7ª propriedade
Ao trocarmos duas linhas ou duas colunas de posição de uma matriz, o valor do seu determinante passa a ser oposto ao determinante da anterior.
8ª propriedade
9ª propriedade
Considerando duas matrizes quadradas de ordem iguais e AB matriz produto, temos que: det (AB) = (det A) * (det B), conforme teorema de Binet.
10ª propriedade
Ao multiplicarmos todos os elementos de uma linha ou de uma coluna pelo mesmo número e adicionarmos os resultados aos elementos correspondentes de outra linha ou coluna, formamos a matriz B, onde ocorre a seguinte igualdade: det A = det B. Esse teorema é atribuído a Jaco.
Exercícios Propostos Determinantes
1) Uma matriz A de ordem n onde aij = 2, para i = j e aij = 0, para i diferente de j. Se o det(3A) = 1296, o n será igual a:
2) Se A é uma matriz quadrada de ordem 2 e det=5, qual é o valor de det(3A).
3) Se A = (aij) é matriz quadrada de ordem 3, tal que aij = i- j, entã pode-se afirmar que o determinante da matriz (5A) é igual a:
Video Sobre Determinantes! Assistam
Determinantes
Determinante de ordem 1
O determinante de ordem 1 é o próprio número da matriz.
Ex:
A= (3)
O determinante será o próprio número 3 det(A) = 3
Determinante de ordem 2
O determinante de ordem 2 se dá a partir da multiplicação dos números existentes na matriz quadrada.
Ex:
Determinantes de ordem 3
Para encontrar o determinante de ordem 3 é necessário que se utilize a regra de Sarrus.
Essa regra diz que deve-se repetir as duas primeiras colunas e multiplica as suas diagonais (principais e secundárias).
Ex:
Determinante maior ou igual a de orem 4
Para se encontrar os determinantes maiores ou iguais a quatro é necessário utilizar o Teorema de Laplace.
Esse teorema diz que o determinante de uma matriz quadrada de qualquer ordem é igual a soma dos produtos dos elementos de uma fila qualquer pelos respectivos cofatores.
Ex:
Cofator
O cofator é definido a partir da seguinte fórmula:
Compreendendo os elementos dessa expressão:
O Aij é o cofator é o elemento aij da matriz A, o Dij é o determinante da matriz obtida através da matriz A. Deverá se excluir da matriz A os elementos da linha i e da coluna j.
Ex:
Multiplicação de matrizes
Multiplicação e realizada de acordo com as seguintes regras :o numero de colunas da 1º matriz deve ser igual ao numero de linhas da 2º matriz. Exemplos:
A4x3 * B3x1
A1x2 * B2x2
Precisamos ter bastante atenção na resolução de uma multiplicação de matrizes,a operação deve ser feita multiplicando os membros da linha da 1º matriz pelos membros da coluna da 2º matriz ,onde os elementos devem ser somados formando uma unica matriz.
Observem o exemplos:
Fizemos uma multiplicação entre uma matriz A de ordem 2x3 por uma matriz B de ordem 3x2 notamos que o número de colunas da 1º matriz dever ser igual o número de linhas da 2º matriz,foi valida pois 3=3.
O interessante é que a matriz ,produto da multiplicação é de ordem 2x2, isto é,2linhas e 2colunas ,possuindo o mesmo número de linhas da 1º e o mesmo número de colunas da 2º.
Portanto devemos observar todas essas condições na hora da multiplicação de matrizes, caso alguma dessas condições não seja valida , a multiplicação ficará errada.
Sempre que realizar multiplicação entre matrizes faça de forma atenciosa ,desenvolvendo completamente o processo.
Equação matricial
Exemplo 1
Encontre a matriz X, que satisfaça a seguinte igualdade X-A=B, onde
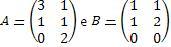
Antes de darmos início ao uso das matrizes, utilizaremos a igualdade dada para isolarmos a nossa incógnita X.

Sendo assim, substituiremos as matrizes que conhecemos nesta equação a fim de encontrarmos a matriz X.

Exemplo 2
Se é possível resolvermos equações matriciais, por que não sistemas de equações matriciais? Vejamos um exemplo:
Determine as matrizes X e Y, que satisfaça o sistema a seguir.

Primeiramente devemos encontrar as relações de X e Y, através do sistema dado, para daí então iniciarmos o cálculo de cada matriz.

Sendo assim, temos duas relações para as matrizes solução.
.png)
Encontrando a matriz Y:
.png)
Encontrando a matriz Y:

Encontrando a matriz X:
.png)
A operação com qualquer matriz sempre resultará em outra matriz, independente da operação utilizada.
Adição e Subtração com Matrizes.
- Adição:
Ou seja:
Se somarmos a matriz A com a matriz B, de mesma ordem, A+B=C, teremos como resultado outra matriz C de mesma ordem para forma e os elementos de C somaremos os elementos correspondentes de A e B. Assim: a11 + b11 = c11
Exemplos:
Dada as matriz A e B, de ordem 3x
A
 +
+  B
BLogo Teremos:
 +
+ =
=
Observe os elementos em destaque:
a13= -1 e b13= -5 ao somarmos esses elementos chegaremos a um terceiro: c13= -6.Pois -1 + (-5) = -1 – 5 = - 6
a13 = - 1 e b13 = - 5 ao somarmos esses elementos chegaremos a um terceiro que é o
c13 = -6. Pois -1 + (-5) = -1 – 5 = - 6
O mesmo ocorre com os outros elementos, para chegarmos ao elemento c32, tivemos que somar a32 + b32. Pois, 3 + (-5) = 3 – 5 = - 2
Assim: A + B = C, onde C tem a mesma ordem de A e B.
- Subtração:
As duas matrizes envolvidas na subtração devem ser de mesma ordem. E a diferença delas deverá dar como resposta da outra matriz, mas de mesma ordem.
Assim teremos:
Se subtraírmos a matriz A da matriz B de mesma ordem, A – B = C, obteremos outra matriz C de mesma ordem. E para formarmos os elementos de C, subtrairemos os elementos de A com os elementos correspondentes de B, assim:a21 – b21 = c21.
Exemplo:
 -
-
Dada a matriz A= 3x3 e B= 3x3, se subtrairmos A-B teremos:
 -
- =
= 3x3
3x3
Observe os elementos destacados:
Quando subtraímos a13 – b13 = c13, -1 – (-5) = -1 + 5 = 4
Quando subtraímos a31 – b31 = c31, - 4 – (-1) = -4 + 1 = -3
Assim A – B = C, onde C é uma matriz de mesma ordem de A e B.
Assim teremos:
Se subtraírmos a matriz A da matriz B de mesma ordem, A – B = C, obteremos outra matriz C de mesma ordem. E para formarmos os elementos de C, subtrairemos os elementos de A com os elementos correspondentes de B, assim:a21 – b21 = c21.
Exemplo:
 -
-
Dada a matriz A= 3x3 e B= 3x3, se subtrairmos A-B teremos:
 -
- =
= 3x3
3x3Observe os elementos destacados:
Quando subtraímos a13 – b13 = c13, -1 – (-5) = -1 + 5 = 4
Quando subtraímos a31 – b31 = c31, - 4 – (-1) = -4 + 1 = -3
Assim A – B = C, onde C é uma matriz de mesma ordem de A e B.
terça-feira, 29 de novembro de 2011
Tipos de matrizes
Uma matriz recebe certo tipo de nome dependendo da quantidade de elementos em suas linhas e colunas ou apenas por características específicas.
- Matriz nula: São matrizes que independente do numero de linhas e colunas todos os seus elementos são iguais zero

- Matriz identidade: ela tem que ser quadrada e os elementos que pertecerem à diagonal principal devem ser iguais a 1 e os restantes dos elementos iguais a zero :
- Matriz transposta: Dada uma matriz A, chamamos de matriz transposta de A à matriz obtida de A trocando-se, "ordenadamente", suas linhas por colunas. Indicamos a matriz trasnposta de A por At.
- Matriz diagonal : É a matriz quadrada que apresenta todos os elementos, não pertendentes à diagonal principal, iguais a zero.
- Matriz triângular: matriz quadrada em que os elementos localizados abaixo ou acima da diagonal principal são nulos
Assinar:
Comentários (Atom)


 ,
,






















